Finite Difference Method (now with free code!)
A couple of months ago, we wrote a post on how to use finite difference methods to numerically solve partial differential equations in Mathematica. Several readers have asked for more details about the method. To help everyone out, we are posting a Mathematica notebook that contains explanations and code. Download the notebook by clicking here.
The notebook implements a finite difference method on elliptic boundary value problems of the form:
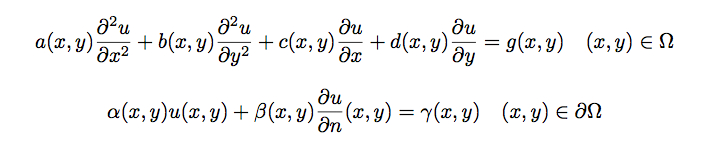
The comments in the notebook will walk you through how to get a numerical solution. An example boundary value problem is solved, yielding a solution that looks like this:

Last week, Mathematica 9 was released. It has some awesome new features, including enhanced NDSolve capabilities. Sadly, there is no built-in finite difference method solver yet. We will have to continue to use workarounds like the notebook posted here for a while longer.
