A skeptical look at The Economist's Sinodependency Index
In a recent blog post, The Economist discusses its “Sinodependency Index”, which measures the world’s economic dependence on China. This index was originally proposed in 2010. In today’s post, we will take a closer look at this index, and in the process, we will explore some of Mathematica’s finance-related capabilities.
The Economist’s Sinodependency Index (SI) is composed of S&P 500 firms, weighted according to their revenues from China. You can see how the SI has outperformed the S&P 500 over the past couple of years, with the implication that firms with more exposure to China are performing better than their less “Sinodependent” peers.
How the SI is calculated
In The Economist’s original formulation of the SI, a firm’s weight was calculated by multiplying its market capitalization by the fraction of its revenue from China. In the new version of the SI, a firm’s weight is simply its revenues from China. Although the two versions are qualitatively similar, we will focus on the original formulation. The reason for this preference is twofold: first, because the original method is based on market capitalization, it provides an apples-to-apples comparison with the S&P 500; second, market capitalization statistics are available on a daily basis, while revenue numbers tend to be released only quarterly.
A fair fight?
At first glance, it seems that the SI’s superior performance in comparison to the S&P 500 can be chalked up to the way that the SI firms are weighted (firms with more exposure to China have higher weights in the SI). On closer examination, though, it seems that the difference between these indices could be a result of sampling bias. The SI is not composed of all 500 of the firms in the S&P index. Instead, it is composed of the 135 firms that The Economist was able to find regional revenue data for. What if these 135 firms did better than the other S&P 500 firms for a reason independent of their Chinese exposure? Let’s try to answer this question.
An aside on journalists posting data sets
The Economist has been kind enough to post a CSV file of the weights it uses in building the SI. They do this to please what they call “data aficionados”. I applaud this approach to financial journalism. It is a great step toward methodological transparency, and it encourages readers to engage with the data. I have a complaint, though. Suppose you stand on a street corner, advertising that you have free gifts for “narcotics aficionados”. If you hand your excited gift recipients cups of coffee, many people will be grateful for your generosity. Don’t be surprised, though, by a few surly looks of disappointment from those jonesing for a black tar heroin fix. Cheers to The Economist for the effort, but I hope that its next gift for aficionados is a much more comprehensive data set.
A better benchmark for the SI
Instead of measuring the SI against the S&P 500, it makes more sense to measure it against an index composed of the same 135 firms, but with a more standard weighting. One logical choice is to make an index of those 135 firms, simply weighted by market capitalization (as S&P does for the full 500 firms). To make this comparison, we need to do a little work in Mathematica.
First, we use the weights provided by The Economist to back-calculate the fraction of revenue that each of the 135 firms gets from China. To do this, we need each firm’s total revenue. We can build a table of current values by accessing Wolfram Alpha, with a command like the following:
revenues =
Table[WolframAlpha[
StringJoin["Revenue ", ToString[k]], {{"Result", 1}, "NumberData"},
PodStates->{"HistoryQuarterly:Revenue:FinancialData__Last 2 years"}], {k,
names}]Here, “names” is a list of the names of the companies. Note that you can avoid having to interface with Wolfram Alpha by using Mathematica’s FinancialData commands, but I find these cumbersome. They require you to deal with the NYSE ticker symbols, instead of company names. I suppose that this is a second language for stock geeks, but sometimes it can get confusing. (For example, who would guess that BEN is the symbol for Franklin Investments? Witty, yes, but it would not have been my first guess).
Once equipped with revenue figures, we can calculate the weights for the original version of the SI.
Next we need market capitalization time series, and again we turn to Wolfram Alpha.
marketcaps =
Table[WolframAlpha[
StringJoin["MarketCap ",
ToString[k]], {{"HistoryDaily:MarketCap:FinancialData", 1},
"TimeSeriesData"},
PodStates->{"HistoryDaily:MarketCap:FinancialData__Last 2 years"}], {k,
names}]Accessing data through Wolfram Alpha is fairly smooth. There is a little bit of data tidying that needs to be done, but most of the work is done for you.
Using the market capitalization time series, we can compare the performances of the SI (or “Sino 135”), the same 500 companies with market cap weighting (Market Cap 135), and the S&P 500.
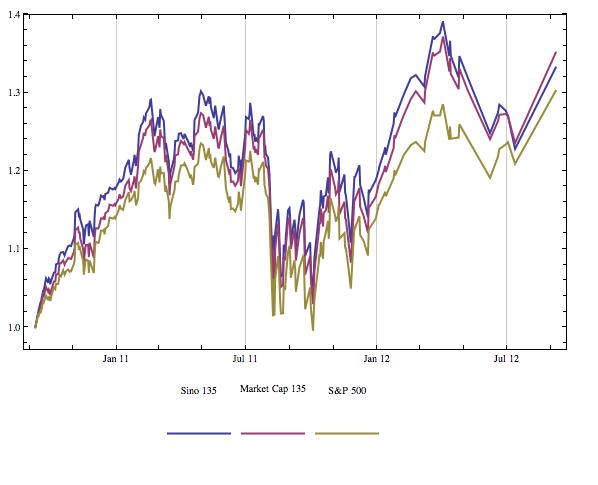
Conclusion:
With this comparison, we can see that the Sinodependency Index has performed similarly to a more standard index of the same 135 companies. This indicates that the magic is not in the SI weights, but in the particular firms included. It could be that the 135 firms that provide regional revenue break-downs happen to be the most China-exposed firms, but this is far from certain. This exercise provides an important lesson: be skeptical, even when dealing with the best media sources.
